| Casio |  Texas |  Géoplan |  Géogébra |  Retour aux cours |  Le Programme |  Activités |  Le cours |  QCM - Vrai-Faux |  Le contrôle |  Aide sur le chapitre | 

I Fonction affine     1. Définition On appelle fonction affine la fonction f qui à tout x de  associe le réel f(x) défini par f(x) = ax + b, a et b étant deux réels. Cas particulier : Si b = 0 alors f est une fonction linéaire.     2. Sens de variation Si a > 0 la fonction affine est croissante sur . Si a < 0 la fonction affine est décroissante sur . Démonstration : Soit f la fonction définie par f(x) = mx + p. Soient a et b deux réels, déterminons f(b) - f(a) f(b) - f(a) = (mb + p) - (ma + p) = m(b - a) Si m > 0 alors f(b) - f(a) et (b - a) ont le même signe donc f est strictement croissante sur . Si m < 0 alors f(b) - f(a) et (b - a) sont de signes contraires donc f est strictement décroissante sur .     3. Signe d'une fonction affine     4. Courbe représentative La courbe représentative de la fonction affine f définie par f(x) = ax + b est la droite d’équation y = ax + b. a est le coefficient directeur, b est l’ordonnée à l’origine. II Fonction carré     1. Définition On appelle fonction carré la fonction f qui à tout x de  associe le réel f(x) défini par f(x) = x2.     2. Sens de variation La fonction carré est croissante sur 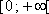. La fonction carré est décroissante sur .          Démonstration : Soit f la fonction définie par f(x) = x2. Soient a et b deux réels, déterminons f(b) - f(a) f(b) - f(a) = b2 - a2 = (b - a)(b + a) 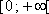Si a et b sont positifs alors b + a est positif donc f(b) - f(a) et (b - a) ont le même signe donc f est croissante sur . Si a et b sont négatifs alors b + a est négatif donc f(b) - f(a) et (b - a) sont de signes contraires donc f est décroissante sur .     3. Courbe représentative La courbe représentative de la fonction carré f définie par f(x) = x2 est la parabole d'équation y = x2. III Fonction inverse     1. Définition On appelle fonction inverse la fonction f qui à tout x de 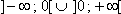associe le réel f(x) défini par f(x) =  .     2. Sens de variation La fonction inverse est strictement décroissante sur et sur .      Démonstration : Soit f la fonction définie par f(x) = . Si a et b sont strictements positifs alors ab est strictement positif donc f(b) - f(a) et (b - a) sont de signes contraires donc f est strictement décroissante sur . Si a et b sont strictements positifs alors ab est strictement positif donc f(b) - f(a) et (b - a) sont de signes contraires donc f est strictement décroissante sur .     3. Courbe représentative La courbe représentative de la fonction inverse f définie par f(x) = est l'hyperbole d'équation y = .