|
|
|
|
|
Vecteurs Définition de la translation qui transforme un point A du plan en un point B. Vecteur 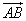 associé. associé.Egalité de deux vecteurs 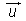 = = 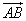 = = 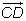 . .Coordonnées d'un vecteur dans un repère. Somme de deux vecteurs. Produit d'un vecteur par un nombre réel. Relation de Chasles. |
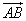 = = 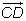 équivaut à ABDC est un parallélogramme, éventuellement applati. équivaut à ABDC est un parallélogramme, éventuellement applati.(xB - xA;yB - yA) du vecteur 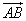 . .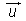 . .
|
A tout pointC du plan, on associe par la translation qui transforme A eb B, l'unique point D tel que [AD] et [BC] ont le même milieu. La somme de deux vecteurs 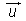 et et 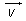 est le vecteur associé à la translation résultant de l'enchaînement des translations est le vecteur associé à la translation résultant de l'enchaînement des translations
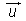 et de vecteur et de vecteur 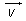 . .Pour le vecteur 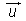 de coordonnées (a ; b) dans un repère, le vecteur k de coordonnées (a ; b) dans un repère, le vecteur k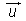 est le vecteur de coordonnées
(ka ; kb) dans le même repère. Le vecteur k est le vecteur de coordonnées
(ka ; kb) dans le même repère. Le vecteur k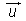 ainsi défini est indépendant du repère. ainsi défini est indépendant du repère.
|