|
I Vocabulaire des événements 1. Expérience aléatoire Une expérience aléatoire est une expérience comportant plusieurs issues. C'est le hasard qui détermine les issues de l'expérience L'univers associé à l'expérience aléatoire est l'ensemble des issues de cette expérience. On le note  . .Un événement est un ensemble d'issues de cette expérience alétoire. C'est une partie de  . .Un événement élémentaire est un événement ne contenant qu'une seule issue pour cette expérience alétoire. L'événement impossible est l'événement ne contenant aucune issue pour cette expérience alétoire. L'événement certain est l'événement contenant toutes les issues pour cette expérience aléatoire. 2. Evénements particuliers L'événement impossible est l'événement ne contenant aucune issue pour cette expérience alétoire. L'événement certain est l'événement contenant toutes les issues pour cette expérience alétoire. L'événement contraire à un événement A est l'événement noté  contenant toutes les issues pour lesquelles A n'est pas réalisé. contenant toutes les issues pour lesquelles A n'est pas réalisé.L'événement 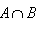 est l'événement constitué de l'événement A et de l'événement B. est l'événement constitué de l'événement A et de l'événement B.L'événement 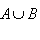 est l'événement constitué de l'événement A ou de l'événement B. est l'événement constitué de l'événement A ou de l'événement B.Exemples :
1. Lien avec les fréquences Lorsque l'on répète une même expérience n fois, les fréquences obtenues pour un événement A se rapprochent d'une valeur théorique lorsque n devient grand. Cette valeur est la probabilité de l'événement A. 2. Loi de probabilité Soit une expérience aléatoire définie sur un univers  . . , c'est associer à chaque événement élémentaire un réel compris entre 0 et 1 tel que la somme des probabilités des événements élémentaires soit égale à 1. , c'est associer à chaque événement élémentaire un réel compris entre 0 et 1 tel que la somme des probabilités des événements élémentaires soit égale à 1.III Calcul de probabilités 1. Equiprobabilité sur un ensemble fini Lorsque tous les événements élémentaires d'un univers 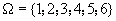 ont la même probabilité, on dit qu'il y a équiprobabilité. ont la même probabilité, on dit qu'il y a équiprobabilité.La probabilité d'un événement A est :  2. Probabilité de la réunion d'événements Soit A et B deux événements,  Cas particuliers : Si 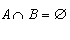 , on dit que A et B sont incompatibles. , on dit que A et B sont incompatibles.On a alors 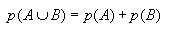 3. Probabilité de l'événement contraire Soit A un événement et  son événement contraire. son événement contraire.Comme 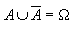 alors alors 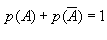 donc donc 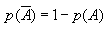 |

