|
I Notion de fonction Une fonction f est un procédé qui permet d'associer à tout réel x, élément d'un ensemble D, un unique réel y. Notation de f  II Courbe représentative Le plan est muni d’un repère. Soit f une fonction définie sur son domaine de définition . On appelle courbe représentative (ou représentation graphique) de la fonction f, notée Cf , l’ensemble des points M ( x ; y ) tels que y = f (x). III Différentes manières de définir une fonction Une fonction peut être définie à l'aide d'une formule, d'une courbe ou d'un tableau de valeurs. 1. A l'aide d'une formule Soit f définie sur [– 3 ; 5] par f (x) = x2 - 4. L'ensemble de définition est Df = [– 3 ; 5]. L'image de 0 est - 4. 2 est un antécédent de 0. 2. A l'aide d'une courbe  L'ensemble de définition est Df = [– 4 ; 2]. L'image de 1 est – 2. Les antécédents de 1 sont – 2 et 0. 3. A l'aide d'un tableau de valeurs. On peut placer les points dans un repère, cela s'appelle un nuage de points ou les relier pour tracer une esquisse de courbe. 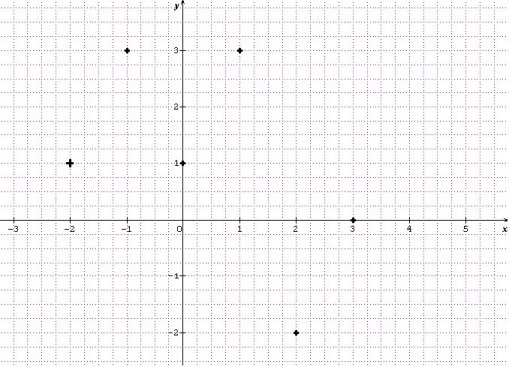 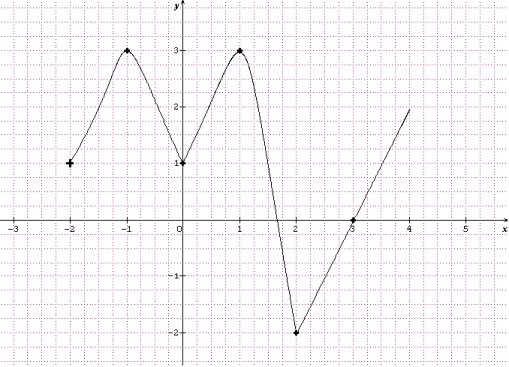 1. Résolution graphique de l'équation f (x) = k (avec k réel) Soit f une fonction et Cf sa courbe représentative.  Les solutions de l'équation f (x) = k sont les abscisses des points d'intersection de Cf avec la droite d'équation y = k (s'ils existent). Pour cet exemple, S = {x1 ; x2} 2. Résolution graphique de l'inéquation f (x) < k (avec k réel) Soit f une fonction et Cf sa courbe représentative. 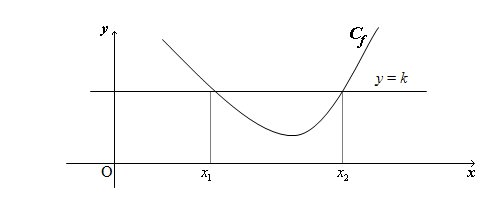 Les solutions de l'inéquation f (x) < k sont les abscisses des points de Cf pour lesquels la courbe Cf est située strictement en-dessous de la droite d'équation y = k. Pour cet exemple, S = ] x1 ; x2[ V Sens de variation d'une fonction 1. Définitions Soit f une fonction et I un intervalle contenu dans son domaine de définition Df. Soient a et b deux réels de I.  2. Notion de maximum et de minimum  3. Tableau de variation d'une fonction 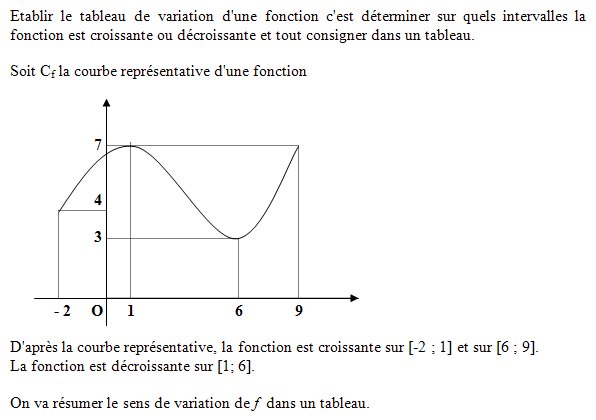  |