| Casio |  Texas |  Géoplan |  Géogébra |  Retour aux cours |  Le Programme |  Activités |  Le cours |  QCM - Vrai-Faux |  Le contrôle | 

I La perspective cavalière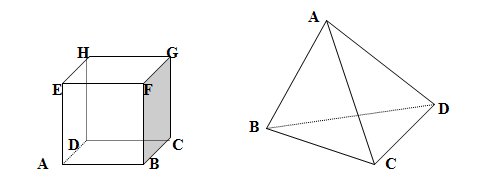 Par convention les segments visibles sont représentés en traits pleins, les autres sont représentés en pointillés. Les droites parallèles dans l'espace sont représentées par des droites parallèles. Dans un plan de face, une figure est représentée en vraie grandeur. Les proportions sur un segment sont respectées. Les angles ne sont représentés en vraie grandeur que dans les plans de face. II Détermination d'un plan Un plan peut être déterminé par : Trois points non alignés ; Une droite D et un point A n'appartenant pas à la droite ; Deux droites parallèles non confondues ; Deux droites sécantes ; III Positions relatives d'une droite et d'un plan    1. Droite et plan sécants 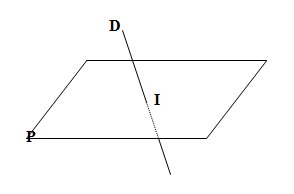L'intersection du plan (P) et de la droite (D) est le point I.    2. Droite parallèle à un plan    a. La droite est contenue dans le plan La droite (D) est parallèle au plan (P) car tous les points de (D) appartiennent à (P).    b. La droite est strictement parallèle au plan 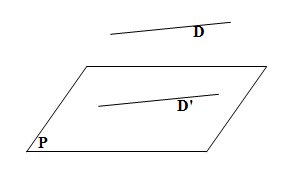La droite (D) est strictement parallèle au plan (P) car (D) et (P) n'ont aucun point commun. Le plan (P) contient une droite (D') parallèle à (D). IV Positions relatives de deux plans    1. Plans sécants Propriété : Si deux plans sont sécants, leur intersection est une droite    2. Plans parallèles 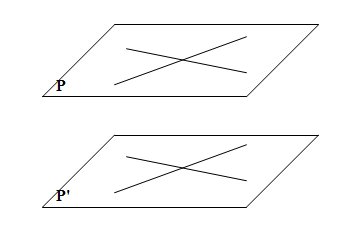Définition : Deux plans sont parallèles s'ils sont confondus où s'ils n'ont aucun point commun. Propriété : Si deux droites sécantes d'un pan (P) sont respectivement parallèles à deux droites sécantes d'un plan (P') alors les plans (P) et (P') sont parallèles. Propriété : Si deux plans sont parallèles alors toute droite contenue dans un des plans est parallèle à l'autre plan. V Positions relatives de deux droites    1. Droites coplanaires 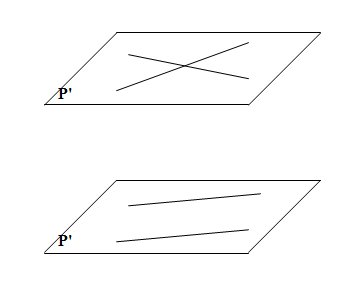Propriété : Deux droites sécantes ou parallèles sont coplanaires    2. Droites non coplanaires 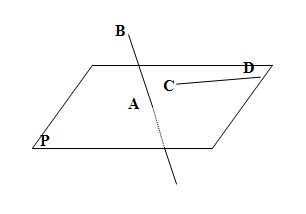Il n'existe pas de plan contenant A, B, C et D. Les droites (AB) et (CD) ne sont pas coplanaires. Propriété : Deux droites non coplanaires ne sont ni sécantes ni parallèles.