| Casio |  Texas |  Géoplan |  Géogébra |  Retour aux cours |  Le Programme |  Activités |  Le cours |  QCM - Vrai-Faux |  Le contrôle |  Aide sur le chapitre | 

I Equations de droites Toute droite D du plan admet une équation de la forme y = mx + p ou bien x = c. Démonstration : Soient A(xA ; yA) et B(xB ; yB) deux points distincts d'une droite (D) et M (x ; y) un point de (D). M appartient à (D) équivaut à et sont colinéaires. En utilisant la condition de colinéarité, on obtient : (x - xA)(xB - xA) - (y - yA)(yB - yA) = 0. En développant, on obtient : x(yB - yA) - y(xB - xA) - xA(yB - yA) + yA(xB - xA) = 0. En posant a = yB - yA et b = - (xB - xA) et c = - xA(yB - yA) + yA(xB - xA), on obtient une équation de la forme ax + by + c = 0 . C'est l'équation cartésienne de (D). Si xA = xB alors (x - xA)(xB - xA) - (y - yA)(yB - yA) = 0 devient x = xA. Toute droite (D) parallèle à l'axe des ordonnées a une équation de la forme x = c. Si xA xB alors (x - xA)(xB - xA) - (y - yA)(yB - yA) = 0 devient : . En développant, on obtient une équation du type y = mx + p avec . m est le coefficient directeur, p est l'ordonnée à l'origine. II Vecteur directeur d'une droite D Toute droite d'équation y = mx + p admet pour vecteur directeur (1 ; m). Démonstration : Si xA = 0 alors les coordonnées de A sont (0 ; p). Si xA = 1 alors les coordonnées de B sont (1 ; m + p). Les coordonnées de sont (1 ; m). est un vecteur directeur de (D). III Droites parallèles Deux droites sont parallèles si et seulement si elles sont toutes les deux parallèles à l'axe des ordonnées ou si elles ont le même coefficient directeur. Démonstration : Si les deux droites sont toutes les deux parallèles à l'axe des ordonnées, elles ont toutes les deux une équation de type x = c donc il est évident qu'elles sont parallèles entre elles puisque toutes les deux parallèles à l'axe des ordonnées. Si les deux droites ne sont pas parallèles à l'axe des ordonnées, alors (D) a pour équation y = mx + p avec pour vecteur directeur (1 ; m) et (D') a pour équation y = m'x + p' avec pour vecteur directeur (1 ; m’). D'après la condition de colinéarité de deux vecteurs, on a (1)(m') – (1)(m) = 0 d'où m = m'. IV Equation linéaire à 2 inconnues Une équation linéaire à 2 inconnues x et y est une équation de la forme ax + by = c avec a, b et c des réels tels que (a ; b) (0 ; 0). Trouver une solution de cette équation, c’est déterminer un couple (x0 ; y0 ) vérifiant cette équation. Exemple : 2x + 3y = 5 admet le couple (1 ; 1) pour solution. Remarque : le couple (4 ; – 1) est aussi solution. V Systèmes linéaires de 2 équations à 2 inconnues Un système de 2 équations à 2 inconnues peut s’écrire sous la forme : Résoudre un tel système, c’est trouver tous les couples (s’il en existe) qui vérifient simultanément les 2 équations.   1. Cas où b 0 et b’ 0 ax + by = c . C’est l’équation réduite d’une droite (D) de coefficient directeur  . a'x + b'y = c' . C’est l’équation réduite d’une droite (D') de coefficient directeur 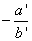 . Résoudre le système (S) revient à déterminer les coordonnées du ou des points d’intersection des droites (D) et (D’) (s’ils existent). 3 cas se présentent : les droites sont sécantes, les droites sont strictement parallèles ou les droites sont confondues. (D) // (D’) = 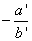soit ab’ – a’b = 0. Le réel ab’ – a’b = 0 est appelé déterminant du système. (D) et (D') se coupent en I (x0 ; y0) ab' - a'b 0 S = {(x0 ; y0)} (D) et (D') sont strictement parallèles ab' - a'b = 0 Le système n'admet pas de couple solution (D) et (D') sont confondues ab' - a'b = 0 Le système admet une infinité de couples solutions 2. Cas où b = 0 ou b’ = 0 Dans le cas où b = 0, l’équation de (D) est ax = c soit . (D) est parallèle à l’axe des ordonnées. Il est plus facile de voir la position des 2 droites (D) et (D’). VI Méthode de résolution de systèmes de 2 équations à 2 inconnues 1. Méthode par substitution Soit à résoudre le système Le déterminant du système est (3)(2) – (5)(–1) = 11. Le déterminant du système n’est pas nul donc le système admet un unique couple solution. On exprime x ou y en fonction de l'autre inconnue dans l'une des équations que l'on remplace par sa valeur dans l'autre équation. Dans la première équation, on obtient y = 3x – 2 Remplaçons y par sa valeur dans la deuxième équation, on obtient : 5x + 2 (3x – 2) = 3 soit 5x + 6x – 4 = 3 , 11x = 7 soit x = Remplaçons x par sa valeur dans y = 3x – 2 Le couple ( ; ) est solution du système. 2. Méthode par combinaisons linéaires Soit à résoudre le système (S) : Le déterminant du système est (5)(– 4) – (3)(2) = – 26. Le déterminant du système n’est pas nul donc le système admet un unique couple solution. Effectuons la combinaison linéaire 2L1 - 5L2 pour éliminer les x 2L1 - 5L2 donne 15x + 6y - 15x + 20y = - 3 - 15 Soit 26y = – 18 donc y = Effectuons la combinaison linéaire 2L1 + L2 pour éliminer les y 2L1 + L2 donne 10x + 4y + 3x - 4y = - 2 + 3 Soit 13x = 1 donc x = Le couple ( ; ) est solution du système.